
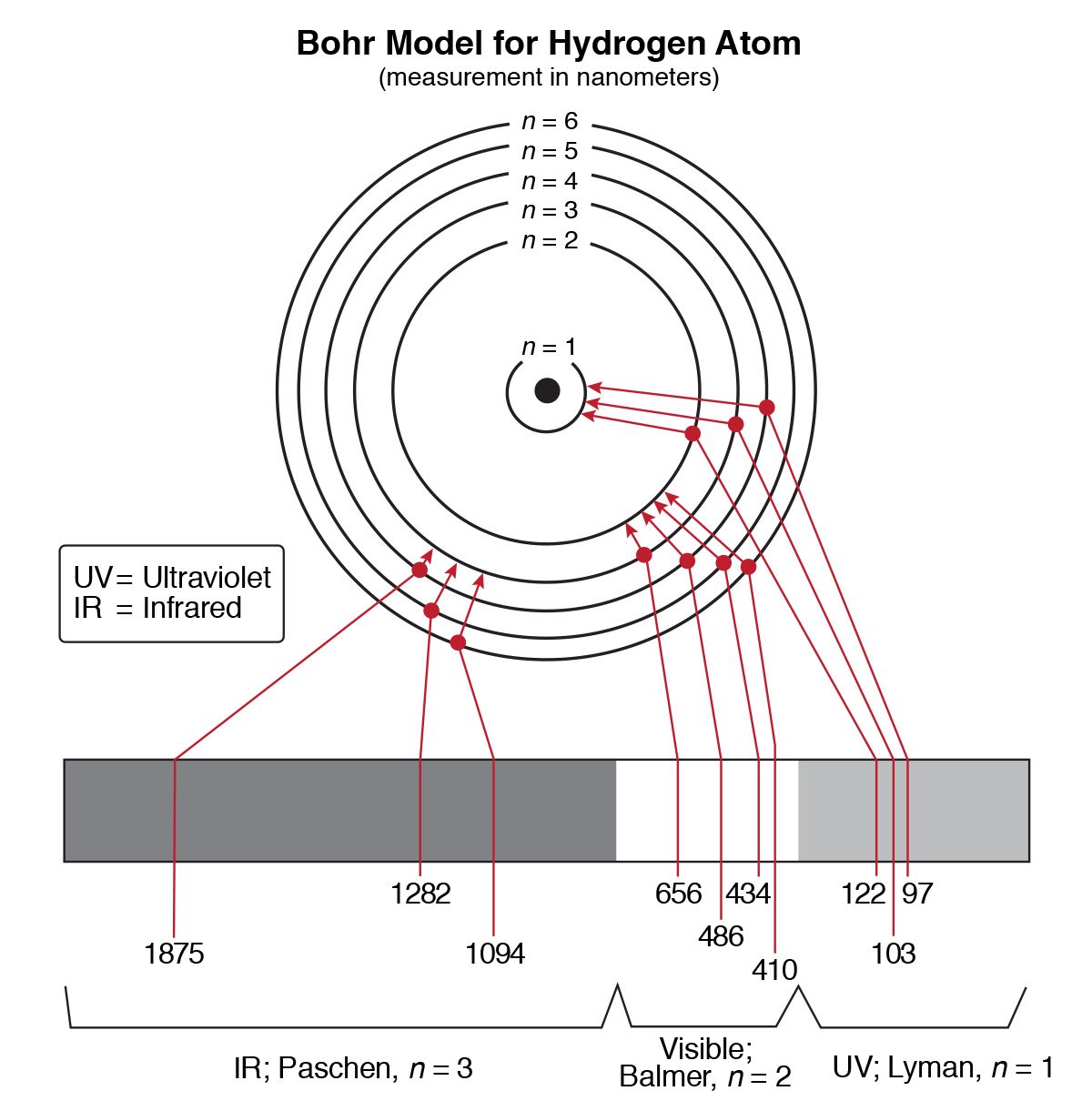
However, the proton is not a point particle and the parameter of non-commutativity is an effective parameter and is not equal to \(-\theta _e\). In fact, for the proton as a point particle \(\theta _p=-\theta _e\) and the corrections on the Coulomb potential coming from both particles cancel. Since all fields live on the same non-commutative space the non-commutativity of a particle not only should be opposite to its antiparticle but also the NC-parameter of a charged particle should be opposite to any other particle of opposite charge. Ho and Kao have shown that there is not any correction on the space–space NC-parameter in this system. However, the effect of NC space on the hydrogen atom at the lowest order is doubtful. There are many studies on the hydrogen atom in the NC space-time.
Here we would like to study the two-body bound state in non-commutative space to explore the differences in the electronic and muonic hydrogen spectrum. Meanwhile, non-commutative standard model (NCSM) via two different approaches is introduced in and its phenomenological aspects are explored in. Theoretical aspects of the non-commutative space have been extensively studied by many physicists. For instance, non-commutative (NC) space can induce new interactions in QED without adding new particles in the theory.
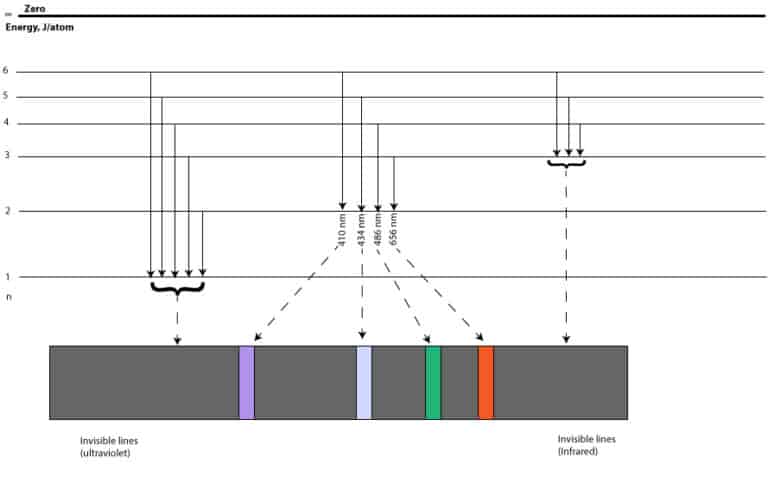
However, the effective new interactions do not necessarily need new particles to mediate the new interactions. There are attempts to explain the new physics by considering a new particle in MeV range where many stringent limits suppress its existence. There are two possibilities to explain the discrepancy: 1-the theoretical calculation within the standard model is incomplete 2-the existence of new physics beyond the standard model. Meanwhile, there is some discrepancy between the recent measurement of the muonic hydrogen Lamb shift and the corresponding proton radius and the CODATA value which is obtained from the spectroscopy of atomic hydrogen and electron–proton scattering. As a simple system, the hydrogen atom with high precision measurements in atomic transitions is one of the best laboratories to test QED and new physics as well.


 0 kommentar(er)
0 kommentar(er)
